Gebrochen-rationale Funktionen
Einleitung
Eine gebrochen-rationale Funktion ist eine Funktion, die aus einem Bruch zweier Polynome besteht, was bedeutet, dass der Zähler und der Nenner jeweils Polynome sind. Man schreibt sie kurz als $f(x)=\dfrac{Z(x)}{N(x)}$ mit den Polynomen $Z$ (wie Zähler) und $N$ (wie Nenner).
Vorab: Hierbei ist es wichtig (das ist schonmal ein kleiner Vorgriff), dass hier der Nenner – also $N(x)$ – nicht Null sein darf. Deshalb gibt es Stellen, an denen die Funktion nicht definiert ist (entweder sind das echte Polstellen oder sog. hebbare Lücken1). Solche gebrochen-rationale Funktionen verhalten sich zumeist wie Polynomfunktionen, zeigen jedoch an den Nullstellen des Nenners ein besonderes Verhalten (z. B. starke Ausschläge oder sog. Asymptoten).
Es gibt verschiedene Arten von gebrochen-rationalen Funktionen, mit denen wir uns Schritt für Schritt in diesem Kapitel beschäftigen werden:
- echt gebrochen-rationale Funktionen sowie
- unecht gebrochen-rationale Funktionen.
In den folgenden Abschnitten werden die wichtigsten Schritte zur vollständigen Funktionsuntersuchung echt sowie unecht gebrochen-rationaler Funktionen systematisch erklärt und an Beispielen angewendet:
- Definitionsbereich und Polstellen bestimmen
- Nullstellen des Zählers und Vorzeichenanalyse für das Vorzeichenverhalten
- Verhalten im Unendlichen: Bestimmung von waagerechten oder schiefen Asymptoten2
- Untersuchung von Polstellen: einfache und mehrfache Pole, (hebbare Definitionslücken) und echte Polstellen
- Differenzialanalyse: erste und zweite Ableitung zum Finden von Monotonie, Extremstellen und Wendepunkten sowie Krümmungsverhalten
- sowie die Skizzierung des Graphen unter Berücksichtigung aller zuvor untersuchter Merkmale und Eigenschaften.
Voraussetzungen hierfür sind:
- Kenntnisse über Polynome,
- Grenzwerte,
- Ableitungen und Vorzeichenuntersuchungen.
Ziel ist es, anhand dieser systematischen Analyse den Graphen einer gegebenen gebrochen-rationalen Funktion zuverlässig zu skizzieren und ihr qualitatives Verhalten vollständig zu beschreiben.
Beispiele für echt sowie unecht gebrochen-rationale Funktionen
Echt und unecht gebrochen-rationale Funktionen
- Ist der Zählergrad kleiner als der des Nenners, so spricht man von einer echt gebrochen-rationalen Funktion.
- Ist der Zählergrad größer oder gleich als der des Nenners, so spricht man von einer echt gebrochen-rationalen Funktion.
Abb. 1: echt gebrochen-rationale Funktion mit waagerechter Asymptote Abb. 2: echt gebrochen-rationale Funktion mit waagerechter Asymptote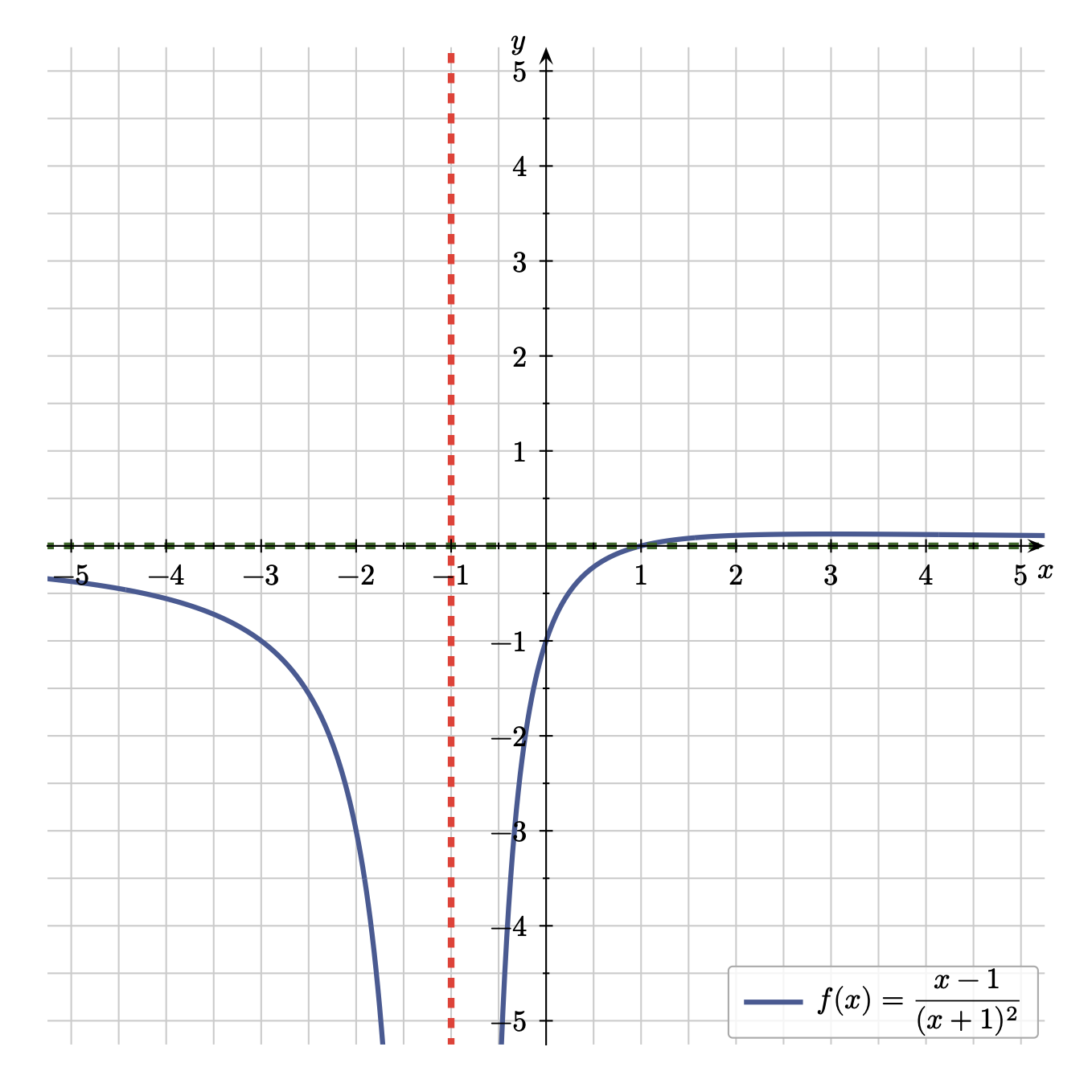
Abb. 3: unecht gebrochen-rationale Funktion mit waagerechter Asymptote Abb. 4: unecht gebrochen-rationale Funktion mit schräger Asymptote


