Zuordnungen und Funktionen
Der Begriff der Zuordnung
Eine Zuordnung ist eine allgemeine Beziehung zwischen zwei Mengen. Sie beschreibt, wie - nicht notwendig allen - Elementen einer Ausgangsmenge $A$ Elemente jeweils ein oder mehrere Elemente aus einer Zielmenge $B$ zugeordnet werden. Eine Zuordnung kann dabei ein- oder mehrdeutig sein. Das bedeutet, dass ein Element aus der Ausgangsmenge durchaus auch mehreren Elementen der Zielmenge zugeordnet sein kann, wie die folgende Abbildung zeigt:
Bildquelle: bettermarks (letzter Aufruf: 13.08.2025)
Verdeutlichung an einem Beispiel
Beispiel #1:
- Menge $A$: Menge an Schülerinnen und Schüler
- Menge $B$: Menge aller Sitzplätze im Klassenzimmer
- Zuordnung $A \rightarrow B$: Den Schülerinnen und Schülern wird ein Sitzplatz zugewiesen.
Wichtig: Im Falle einer Zuordnung wie dieser darf es vorkommen, dass Sitzplätze frei bleiben, Schülerinnen und Schüler leer ausgehen (also keinen Sitzplatz erhalten) oder zwei oder mehrere Schülerinnen und Schüler ein und demselben Sitzplatz zugewiesen werden.
Darstellungsformen
Es gibt verschiedene Darstellungsmöglichkeiten von bzw. für Zuordnungen:
- Wortbeschreibungen wie z.B.: $$\text{“Jeder Schüler bekommt einen Sitzplatz.”}$$
- Zuordnungstabellen:
Schüler A B C D E F … Sitzplatz 1 17 3 5 2 20 …
- Pfeildiagramme (siehe Abb. 1)
- Graphen im Koordinatensystem:
Der Funktionsbegriff
Merke dir:
Eine Funktion ist eine eindeutige Zuordnung. Der Begriff ist wie folgt definiert:
Jedem $x$-Wert (Eingabewert bzw. Argument) wird genau ein $y$-Wert (Ausgabe- bzw. Funktionswert) zugeordnet.
Notation:
- $f(x)$ oder $y=f(x)$
Beispiel:
- $f(x)=2x+3 \rightarrow$ Einsetzen von $x=4$ ergibt $f(4) = 2 \cdot 4 + 3 = 11$.
Veranschaulichung
Im Grunde kannst dir eine Funktion ein wenig so wie eine Maschine bzw. eine blackbox vorstellen:
Bildquelle: madipedia (letzter Aufruf: 13.08.2025)
Das passiert hier also:
- Der Eingabewert $x$ wird oben in diese Maschine hineingeworfen.
- Dieser wird dann durch die Funktion $f$ verarbeitet.
- Der Funktionswert $f(x)$ wird unten ausgegeben.
Nachgedacht:
Mach dir folgende Dinge klar:
- Was passiert, wenn der Wert $x=5$ eingegeben wird und die Funktionsvorschrift $f(x)=3x-4$ lautet?
- Welchen Wert muss man in die Funktion $f(x)=2x+3$ eingegeben, um den Wert $33$ zu erhalten?
- Was passiert, wenn man mehrmals hintereinander denselben Wert “eingibt”?
Wichtige Begriffe im Zusammenhang mit Funktionen
Merke dir:
Im Zusammenhang mit Funktionen solltest du dir die folgenden Begriffe merken:
- die Definitionsmenge beschreibt die Menge aller möglichen Eingabewerte $x$
- der Begriff der Wertemenge beschreibt die Menge aller möglichen Ausgabe- bzw. Funktionswerte $y$
- die Funktionsvorschrift ist die „Rechenregel“, wie bspw. $f(x)=2x+3$, nach der der Eingabewert “verarbeitet” wird
Zurück zum Beispiel
Um den Unterschied zwischen einer Zuordnung und einer Funktion verstehen zu können, schauen wir uns noch einmal das erste Beispiel von vorhin an und modifizieren es nun:
Beispiel #1 - in abgewandelter Form:
Menge $A$: Menge an Schülerinnen und Schüler
Menge $B$: Menge aller Sitzplätze im Klassenzimmer
Funktion $A \rightarrow B$: Jeder Schülerin bzw. jedem Schüler wird genau ein Sitzplatz fest zugewiesen.
Wichtig: Wenn es sich - wie in diesem veränderten Beispiel - um eine Funktion handelt, dann dürfen zwar auch Sitzplätze frei bleiben, jedoch darf es keine Schülerin bzw. keinen Schüler geben, der oder dem kein Sitzplatz zugewiesen wird. Es darf sogar vorkommen, dass alle Schülerinnen und Schüler denselben Sitzplatz zugewiesen bekommen.
Merke dir:
Jede Funktion ist eine Zuordnung, aber nicht jede Zuordnung ist eine Funktion.
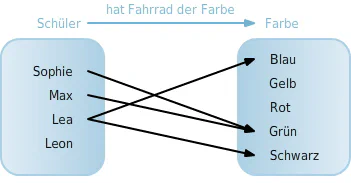 Abb. 1: Pfeildiagramm
Abb. 1: Pfeildiagramm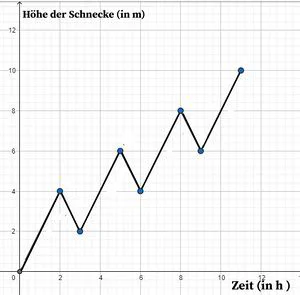 Abb. 2: Graph einer Zuordnung
Abb. 2: Graph einer Zuordnung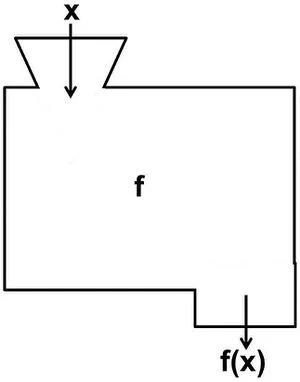 Abb. 3: “Funktions-Maschine”
Abb. 3: “Funktions-Maschine”